Picking Winners with Random Number Generators
While running a promotion using Rafflecopter, a customer can pick random winners while the giveaway is running or after it’s over. We care a lot about making sure these randomly chosen winners are completely unbiased. That means an entrant should be favored to win strictly based on the number of entries that they have in the giveaway. It shouldn’t matter when the entries occurred, what the entrant’s name is (yes, we’ve been accussed of this one smh), what the weather was like, how many spots there were on the sun, etc. Among other things, this requires a high-quality source of random numbers. Hopefully, in a future post, we’ll discuss the tricks we’ve discovered for structuring our data to make winner picking fast and robust. However, this post will focus on a topic that’s interesting and challenging all on its own–random numbers!
Motivated mostly by tradition, we pick winners using numbers from random.org. random.org is a very popular choice for random drawings, and it’s surely a safe one. Their numbers originate from radio receivers listening to atmospheric noise. Unfortunately, if for some reason we’re unable to contact random.org or their system is overloaded, we would have to tell our users to try again later. We view this as an unacceptable user experience especially when psuedorandom number generators (PRNG) exist that satisfy very high standards of statistical quality. In fact, it could be argued that the latest PRNGs are held to even higher standards than the numbers generated by random.org’s true random number generator.
I’d also like to mention another reason that we may elect to use PRNGs in some situations over random.org. When pulling integers from random.org, the largest range available is [0,1e9). In certain situations, we need a larger range of possibilities to avoid collisions. Although it’s possible to pull multiple random numbers and scale them to the desired range, this can be error prone. Also, the lack of transparency from random.org about how exactly consecutive numbers are generated makes this an undesireable approach.
What is a PRNG anyway?
A PRNG is a simple algorithm that calculates the next number in a sequence based on the numbers that came before. A “seed” is an arbitrary number (sometimes multiple numbers) that we give the algorithm to kick-off the calculation. With the right algorithm, these sequences are indistinguishable from natural sources of uniform randomness like atmospheric noise. Let’s look at a simple and obviously terrible PRNG: the fibonacci sequence. The fibonacci sequence was never intended to be a PRNG, but let’s just use it as an example. Remember, that each number in the fibonacci sequence is the sum of the two numbers that came before it.
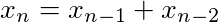
Let’s create a sequence using this recurrence relation. We’ll take the modulus of each number in the sequence to keep the numbers to a manageable size. Then, we’ll treat each three consecutive numbers in the sequence as the x, y and z coordinates of a point in a 3D scatter plot.
%matplotlib notebook
import numpy as np
import matplotlib
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# Silly fibonacci generator
N = 999
seed1 = 0
seed2 = 1
seq1 = [0] * N
for k in range(N):
new_seed = seed2 + seed1
seed1 = seed2
seed2 = new_seed
seq1[k] = new_seed % 1000
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(seq1[0::3], seq1[1::3], seq1[2::3])
print(seq1[0:100])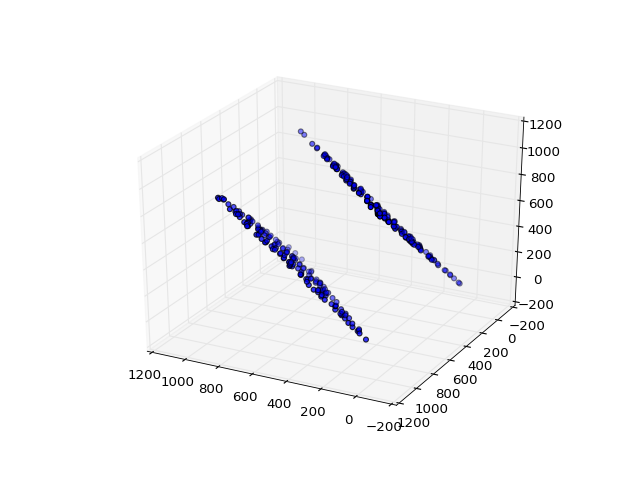
[1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 597, 584, 181, 765, 946, 711, 657, 368, 25, 393, 418, 811, 229, 40, 269, 309, 578, 887, 465, 352, 817, 169, 986, 155, 141, 296, 437, 733, 170, 903, 73, 976, 49, 25, 74, 99, 173, 272, 445, 717, 162, 879, 41, 920, 961, 881, 842, 723, 565, 288, 853, 141, 994, 135, 129, 264, 393, 657, 50, 707, 757, 464, 221, 685, 906, 591, 497, 88, 585, 673, 258, 931, 189, 120, 309, 429, 738, 167, 905, 72, 977, 49, 26, 75, 101]The numbers in the sequence almost look random once we get past the initial ten values or so. However, when we look at the scatter plot, all the points exist on two 2D planes. In other words, there’s a correlation between the x, y and z coordinates. This is probably obvious since consecutive numbers are related to each other by simple addition. We’d like our random numbers to be uniformly distributed throughout the 3D space, and that’s really just a bare-minimum requirement. Let’s move on and take a look at RANDU–a very simple linear congruential generator used in many IBM mainframes in the 60s and 70s that turned out to be fatally flawed.
Each number in the RANDU sequence can be calculated using the following recurrence relationship.
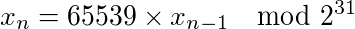
In other words, we multiply the previous number by 65,539 and then take it modulo 2^31. This is beautifully simple, but we’ll see why it’s terrible.
# RANDU algorithm
N = 9999
seq2 = [1] * N
latest_value = 1
for k in range(N):
latest_value = 65539 * latest_value % (2**31)
seq2[k] = latest_value
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(seq2[0::3], seq2[1::3], seq2[2::3])
print(seq2[0:10])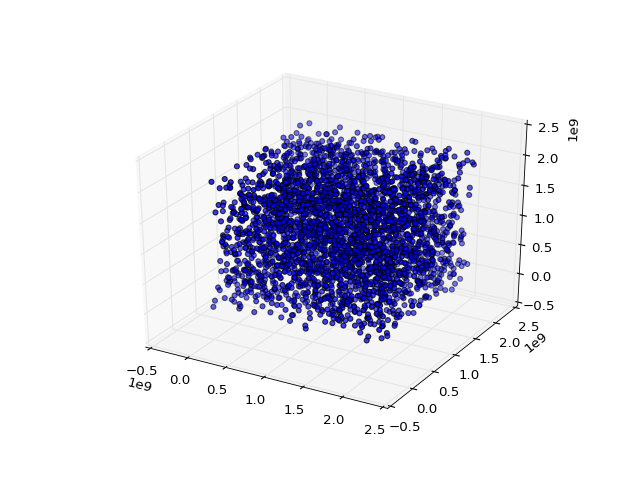
[65539, 393225, 1769499, 7077969, 26542323, 95552217, 334432395, 1146624417, 1722371299, 14608041, 1766175739, 1875647473, 1800754131, 366148473, 1022489195, 692115265, 1392739779, 2127401289, 229749723, 1559239569, 845238963, 1775695897, 899541067, 153401569, 1414474403, 663781353, 1989836731, 1670020913, 701529491, 2063890617, 1774610987, 662584961, 888912771, 1517695625, 1105958811, 1566426833, 1592415347, 1899101529, 1357838347, 1792534561, 682145891, 844966185, 1077967739, 1010594417, 656824147, 1288046073, 1816859115, 1456223681, 975544643, 1337189321, 1390717787, 604570129, 1848378931, 1354175129, 79574987, 1174775649, 2037511715, 1652089449, 164865851, 1152775601, 1137893651, 747348793, 685500843, 1681833217, 1774008067, 1950000393, 28897051, 1950731601, 706897907, 1717188569, 1793566603, 1749153441, 795272163, 1914153897, 32506619, 147523825, 592583379, 80302201, 1591013739, 233428033, 2113830083, 1992193609, 1518625499, 1919428753, 2143910323, 2031054105, 1481066315, 1344329185, 1178829219, 1416463593, 36802235, 357542961, 1814037651, 1223888313, 1754409259, 1658944385, 606433923, 1593005961, 1952646811, 1673794513]At first glance, things look pretty good–pretty random. Let’s rotate the view of the scatter plot a little bit.
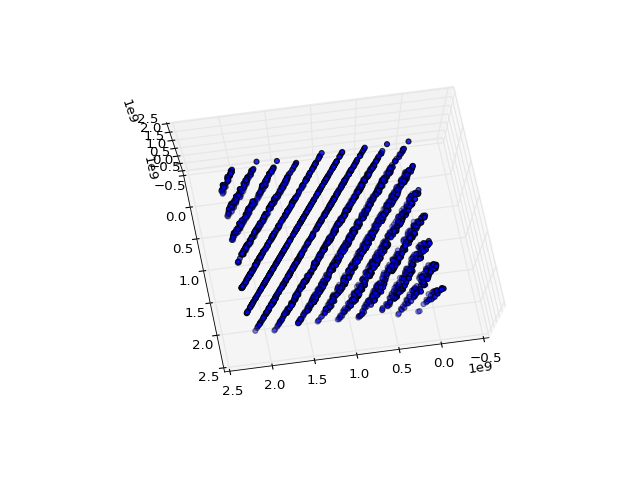
OOPS! All the points live in fifteen 2D planes!
As a result of the wide use of RANDU in the early 1970s, many results from that time are seen as suspicious.
– https://en.wikipedia.org/wiki/RANDU
Yikes. Dealing with randomness can be like walking through a mine field. It’s not just when dealing with PRNG’s either. Natural sources of randomness can be subject to instrumentation glitches, post-processing bugs, and attacks. On a more positive note, PRNG’s have been subjected to more and more rigorous tests over the years. testu01, dieharder, and NIST STS put PRNG’s through a gauntlet of statistical tests.
The statistical quality of random number generators isn’t just abstract, ivory tower nonsense that the average developer can ignore. Consider the case where the Betable team, using Math.random() in nodejs and chrome’s v8 engine, began experiencing hash collisions at a rapid rate. It was found that the multiply-with-carry method in v8’s PRNG had a terrible flaw that cut its range down from 2^32 possible values to 2^16 in certain situations. The v8 team addressed the issue and also found that v8’s PRNG performed very poorly under testu01. New versions of v8 are shipping with xorshift128+.
A final note: it isn’t just a matter of picking the best random number generator. Programmers should be very careful with what they do with random numbers after they receive them from the generator. For example, in the Betable article, it was the MDN recommended multiple-and-floor method, for converting a random float into an integer, that cropped off the lower 16 bits of the number returned from Math.random. In general, play it safe and don’t try anything unneccessarily fancy. If random integers need to be rescaled, use a proven method.
In the past, Rafflecopter has used the mersenne twister alogorithm when we needed to reach for a PRNG. It’s a good algorithm, but it doesn’t perform quite as well on the tests as some of the newer PRNGs. Moving forward, we’ll be using xorshift128+, and algorithms for winner picking will be as simple as they can be while providing the best possible experience for our customers.
Feel free to shoot any questions or feedback for this article over to @justinratner.